152L & 272 L home | 151L & 170L home
  • Propagation of errors (For independent variables only)
Now that you know what the error in a single measurement is, you should ask yourself: "What happens when I add two values with uncertainty?" Anotherwords, how do errors propagate through alegebraic expressions?

I will not cover the reasoning behind this section. (For further info see Taylor's Error Analysis).  Instead I will simply give you the results:
  • Propagation rules for 151 / 152 / 170 / 272:
In all of the following x, y, and z are used to denote data values.   x, y, and z denote uncertainties in those values.  Further examples can be found in the examples section.

    Addition and Subtraction:
      If your equation is z = x + y or z = x - y, the error in z is:
    Multiplication and Division:
If your equation is z = xy or z = x/y, the error in z is:

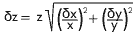
    Powers:
If your equation is z = xn ym, the error in z is:
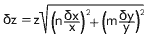
  • Propagation rules for 274 (advanced)
For all equations where the variables x, y, ...., z are independent and have uncertainties  x,  y, ..., z, the function f(x, y, ..., z) has an error which is given by:



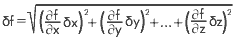
where  is the partial derivative of the function with respect to x, etc.


Examples(for more see Example section)

Addition and Subtraction
x = time 1 = 12.8 +/- 0.2 s
y = time 2 = 8.5 +/- 0.1 s
What is the uncertainty in z = x+y?

Using the formula on the left, we know that the uncertainty in z is
= root( (0.2s)2 + (0.1s)2)
= root(0.05 s2)
= 0.2236 s

z = (12.8 + 8.5) +/- 0.2236 s
So you should report z = 21.3 +/- 0.2

Multiplication and Division

Using the same x and y as before, what is the uncertainty in z = x/y?

The uncertainty in z is
= (z) * root ( (0.2s/12.8s)2 + (0.1s/8.5s)2 )
= (z) * root (0.0003825)
= (12.8 s / 8.5 s) * 0.01956
= 0.02945
So you should report z = 1.51 +/- 0.03 (no units)

Powers:

What is the uncertainty in z = x2y3?
The uncertainty in z is:
= (z) * root ( (2 * 0.2s/12.8s)2 + (3 * 0.1s/8.5s) 2 )
= (z) * root (0.002222)
= ( (12.8s)2 * (8.5s)3) * 0.0471
= 100618.24 s5* 0.0471
=  4743.205 s5
So you should report z = (10.0 +/- 0.5) E4 s5
(Where E4 stands for *104)