The pre-lab and the instructions for the pre-lab are located at http://www2.hawaii.edu/~jmcfatri/labs/circuitprelab.html . The pre-lab is due at the beginning of the class. All students must do the pre-lab exercise.

The objectives of this lab are:

1) to construct an Ohmmeter (a device that measures resistance) using our knowledge of Ohm's Law.
2) to determine an unknown resistance using our Ohmmeter.
3) to verify Ohm's law.
4) to verify Kirchhoff's Rules by adding the voltage differences around a loop and by adding currents going in and out of a junction.

In the last lecture, we saw that the voltage (or the potential difference) was related to energy by the equation W = qV. One way to lose energy in a circuit is to add a resistor.  The potential drop across a resistor is given by Ohm's Law: V= IR where I is the current (in Amps) and R is the resistance (in Ohms)

Kirchhoff's Rules are a set of two rules which, along with Ohm's Law, allow you to solve for the current, voltage, or resistance of a circuit. 

Kirchhoff's Rule #1--The Junction Rule: When wires meet at an intersection, the sum of all the currents going through the intersection must equal zero. Put another way:

the current going in = the current going out

This is just another way of saying that charge is conserved.

Kirchhoff's Rule #2--The Voltage Rule:  The sum of the voltages gained or lost in a circuit loop must equal zero.  Put another way:

the energy gained = the energy lost when going around a loop.

As electrons go across a battery they gain electrical potential energy.  As they go across a resistor, they lose that energy.  The energy lost should equal the energy gained, so that when they come back to the same point (i.e. they go in a loop) they should have the same energy as before.

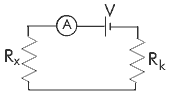
Using the circuit shown, the result of Kirchhoff's Laws are:

V = IR _x + IR_k Rearranging this formula for R_x, an unknown resistor, in terms of R_k , a known resistor, and V, a known voltage source (a battery), we easily obtain:

R_x = V/I - R_k

We know R_k (it is given). We can measure the voltage, V, with a voltmeter and we can measure the current, I, using a galvanometer. The current is proportional to the deflection of the needle in the galvanometer: G = kI where k is just some constant of proportionality. Plugging this in, we have the equation: R_x = (kV)/G - R_k which is a linear equation (of the form y = mx + b).  Unfortunately you don't know the constant of proportionality (and I'm not telling!). Since you don't know k, you have to first figure it out by trying some known R _x . Once you have k, then you can use your ohmmeter with an unknown  R _x.

Verifying Kirchhoff's Rules:

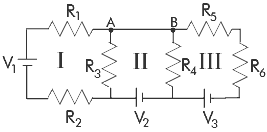
We want to verify Kirchhoff's two rules. First we will verify the voltage rule by measuring the voltages around the loops I, II, and III. (Remember that you don't know theoretically which way the current will flow at this point). Second we will verify that the current coming into node A equals the current going out of node A, and the same for B.

What are the three equations you get from the Voltage Rule?





What are the two equations you get from the Current Rule? 

Part I: Constructing an Ohmmeter:

Obtain: 1 tester board, 1 galvanometer, 5 different resistors (R_x ), and a R_k resistor of 1.8 k (Brown-Grey-Red-Gold resistor code)

1) Create the ohmmeter circuit on the tester board.  Determine the correct configuration on your tester board, in the same way you did in the pre-lab. Draw out a diagram of the tester board below.

2) Choose  R _k = 1.8 k (or Brown-Grey-Red)

3) Calibrate your ohmmeter by using 5 known values of R_x and creating a plot of  R _x versus 1/G.  Use resistor ( R _x ) values 1.5k, 1.8k, 2.7k, 3.9 k, and 6.8 k.  (Other values of  R_x may be substituted in the event that we run short of resistors, as long as you get five distinct points of the range 10 k.)

4) Obtain a regression line slope and y-intercept, using the GA program on the computer. From this plot you can obtain the value of k and the measured value of  R _k.

5) Obtain an unknown resistor and use your graph to determine the resistance. Use your slope and intercept from step 4 to do this.

Part II: Verifing Kirchhoff's Rules:

1) Create the circuit shown in class on the testor board.  All the resistors should have a resistance of 2.2 k (Red-Red-Red-Gold) .  Before you start constructing your circuit, draw a diagram of your tester board below:

 
 

 

 
 

2) Check your circuit!  Make sure your batteries are not getting hot.  If they are, then your batteries are backwards.  While Kirchhoff's Laws are still correct even for this configuration, you risk causing battery leakage by running them the wrong way.

3) Find the voltage across all the batteries and the resistors. Follow the directions given in the pre-lab concerning the use of multimeters.

4) Find the direction and magnitude of the currents going into and out of the nodes marked A and B. Follow the directions given in the pre-lab concerning the use of multimeters.

IMPORTANT!!: DO NOT PUT YOUR MULTIMETER IN PARALLEL WITH ANY COMPONENT WHEN YOU ARE ON THE CURRENT SETTING.  THIS WILL DAMAGE THE METER.  (You may find that some of the meters are damaged already, because of careless students.  If this is the case, you will always read 0 A.  Let me know immediately, so that you can get another meter.)

5) Before you leave, make sure you turn off the multimeter.

Part I: Constructing an Ohmmeter

R_k:_____________+/-_________ (given value)
color code of the unknown resistor: __________________________
Voltage of the battery: :_____________+/-_________ (measured, not assumed)

G for unknown resistor:__________________
1/G for unknown resistor:_________________
k :_____________+/-_________ (from graph)
R_unknown :_____________+/-_________ (from graph)
R_k:_____________+/-_________ (from graph)

Voltage Rule

1. In part II of the experiment, you should have noticed that one of the resistor voltages you measured was positive instead of negative. Does this mean that an electron is gaining energy when it goes through this resistor? Explain.







2. If your experiment showed that the currents going into and out of a junction did not sum to zero within your error range, does that mean that Kirchhoff's Rule #1 is not true for your circuit? What could cause the non-zero sum that you observed? Explain.







3. Why should a voltmeter have a high resistance? Why should an ammeter have a low resistance? (Hint: A meter should be "invisible" to the circuit. It should not change the voltage or current of the element it is reading.)  You may want to draw some simple circuits.