For Printing

Quantitative Facts about Binary Trees

A binary tree is a finite set of vertices that is either empty or consists of a vertex called the root, together with two binary subtrees that are disjoint from each other and from the root and are called the left and right subtrees.

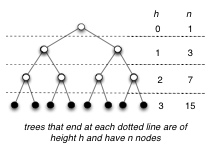
A full binary tree is a binary tree in which each node either is a leaf or has exactly two nonempty descendants. In a full binary tree of height h:

1. # leaves = (# internal nodes) + 1.
2. # leaves is at least h+1 (first example figure) and at most 2^h (second example figure).

3. # internal nodes is at least h (first example) and at most 2^h-1 (second example).
4. Total number of nodes (summing the last two results) is at least 2h+1 (first example) and at most 2^h+1-1 (second example).
5. Height h is at least lg(n+1)-1 (second example) and at most (n-1)/2 (first example)

A complete binary tree is full binary tree in which all leaves have the same depth and all internal nodes have degree 2 (e.g., second example above).

(Note: some earlier texts allow the last level of a "complete" tree to be incomplete! They are defined as binary trees with leaves on at most two adjacent levels l-1 and l and in which the leaves at the bottommost level l lie in the leftmost positions of l.)