Today's Theme: Relax!
or how to get there from here ...
Input is a directed graph G = (V, E) and a weight function w: E → ℜ.
Define the path weight w(p) of path p = ⟨v0, v1, ... vk⟩ to be the sum of edge weights on the path:
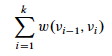
Then the shortest path weight from u to v is:
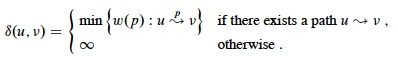
A shortest path from u to v is any path such that w(p) = δ(u, v).
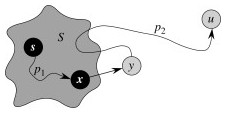
In our examples the shortest paths will always start from s, the source. The δ values will appear inside the vertices, and shaded edges show the shortest paths.
As can be seen, shortest paths are not unique.
These are OK as long as no negative-weight cycles are reachable from the source s. Fill in the blanks:
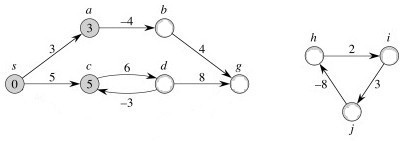
If a negative-weight cycle is accessible, it can be iterated to make w(s, v) arbitarily small for all v on the cycle:

Some algorithms can detect negative-weight cycles and others cannot, but when they are present shortest paths are not well defined.
Shortest paths cannot contain cycles.
The shortest paths problem exhibits optimal substructure, suggesting that greedy algorithms and dynamic programming may apply. Turns out we will see examples of both (Dijkstra's algorithm in this chapter, and Floyd-Warshall in the next chapter, respectively).

Lemma: Any subpath of a shortest path is a shortest path.
Proof is by cut and paste. Let path puv be a shortest path from u to v, and that it includes subpath pxy (this represents subproblems):
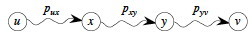
Then δ(u, v) = w(p) = w(pux) + w(pxy) + w(pyv).
Now, for proof by contradiction, suppose that substructure is not optimal, meaning that for some choice of these paths there exists a shorter path p'xy from x to y that is shorter than pxy. Then w(p'xy) < w(pxy).
From this, we can construct p':
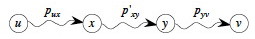
Then
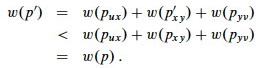
which contradicts the assumption that puv is a shortest path.
All the algorithms we consider will have the following in common.
For each vertex v ∈ V, we maintain these attributes:
v.d is called the shortest path estimate.
v.π = the predecessor of v by which it was reached on the shortest path known so far.
All the shortest-paths algorithms start with this:
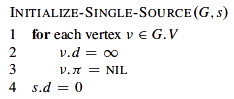
They all apply the relaxation procedure, which essentially asks: can we improve the current shortest-path estimate for v by going through u and taking (u, v)?
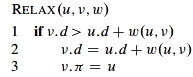

The algorithms differ in the order in which they relax each edge and how many times they do that.
All but the first of these properties assume that INIT-SINGLE-SOURCE has been called once, and then RELAX is called zero or more times.

Proofs are available in the text. Try to explain informally why these are correct.
Essentially a brute force strategy: relax systematically enough times that you can be sure you are done.

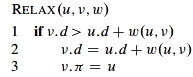
The first for loops do the work of relaxation. How does the last for loop help -- how does it work?
RELAX is O(1), and the nested for loops relax all edges |V| - 1 times, so BELLMAN-FORD is Θ(V E).
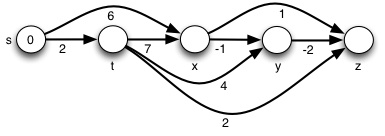
Example from the text, relaxed in order (t,x), (t,y), (t,z), (x,t), (y,x) (y,z), (z,x), (z,s), (s,t), (s,y):
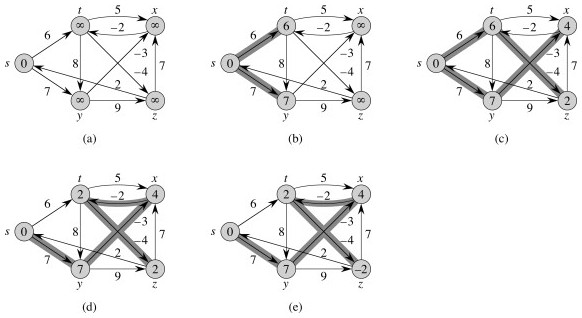
Try this other example (click for answer):


The values for v.d and v.π are guaranteed to converge on shortest paths after |V| - 1 passes, assuming no negative-weight cycles.
This can be proven with the path-relaxation property, which states that if we relax the edges of a shortest path ⟨v0, v1, ... vk⟩ in order, even if interleaved with other edges, then vk.d = δ(s,vk) after vk is relaxed.

Since the list of edges is relaxed as many times as the longest possible shortest path (|V|- 1), it must converge by this property.
We also must show that the True/False values are correct. Informally, we can see that if v.d is still getting smaller after it should have converged (see above), then there must be a negative weight cycle that continues to decrement the path.
The full proof of correctness may be found in the text.
The values computed on each pass and how quickly it converges depends on order of relaxation: it may converge earlier.
How can we use this fact to speed the algorithm up a bit?


Life is easy when you are a DAG ...
There are no cycles in a Directed Acyclic Graph. Thus, negative weights are not a problem. Also, vertices must occur on shortest paths in an order consistent with a topological sort.
We can do something like Bellman-Ford, but don't need to do it as many times, and don't need to check for negative weight cycles:

Given that topological sort is Θ(V + E), what's the complexity of DAG-SHORTEST-PATHS? This one's on you: what's the run-time complexity? Use aggregate analysis ...
Because we process vertices in topologically sorted order, edges of any path must be relaxed in order of appearance in the path.
Therefore edges on any shortest path are relaxed in order.
Therefore, by the path-relaxation property, the algorithm terminates with correct values.

From the text:
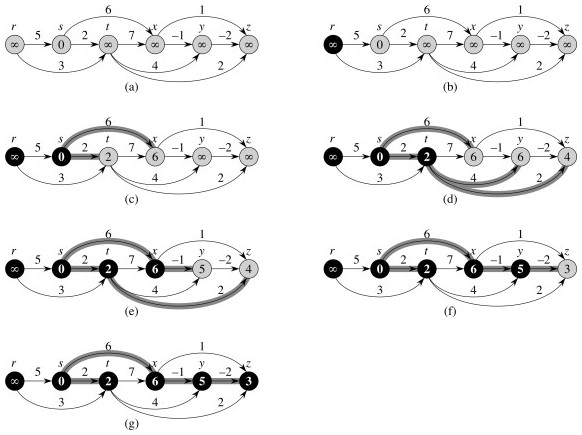
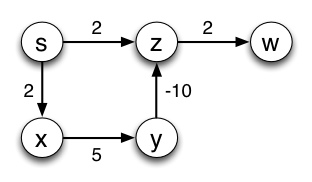
Notice we could not reach r!
Let's try another example (click for answer):

The algorithm is essentially a weighted version of breadth-first search: BFS uses a FIFO queue; while this version of Dijkstra's algorithm uses a priority queue.
It also has similarities to Prim's algorithm, being greedy, and with similar iteration.
Assumes there are no negative-weight edges.
Here it is, with Prim on the right for comparison:

Note, Relax(u,v,w) updates the shortest path estimates v.d of the vertices that are in the priority queue. To make sure the keys of the priority queue are updated properly, we must rewrite Relax(u,v,w) to call DecreaseKey() operation on the vertex being updated:
Relax(u,v,w) 1 if v.d > u.d + w(u,v) 2 DecreaseKey(Q, v, u.d+w(u,v)) // update the key v.d in the priority queue to the new estimate 3 v.π = u
Dijkstra's algorithm is greedy in choosing the closest vertex in V - S to add to S each iteration. The difference is that
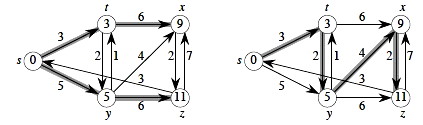
From the text (black vertices are set S; white vertices are on Q; shaded vertex is the min valued one chosen next iteration):
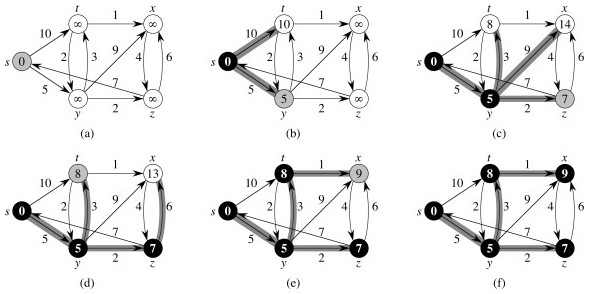
Let's try another example (click for answer):

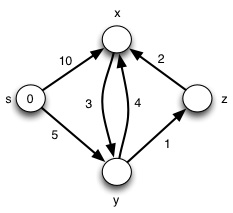
Here's a graph with a negative weight: try it from s and see what happens:

The proof is based on the following loop invariant at the start of the while loop:
v.d = δ(s, v) for all v ∈ S.
Initialization: Initially S = ∅, so trivially true.
Maintenance: We just sketch this part (see text for a rigorous proof). Need to show that u.d = δ(s, u) when u is added to S in each iteration. The upper bound property says it will stay the same thereafter.
Suppose (for proof by contradiction) that ∃ u such that u.d ≠ δ(s, u) when added to S. Without loss of generality, let u be the first such vertex added to S.

Termination: At the end, Q is empty, so S = V, so v.d = δ(s, v) for all v ∈ V
(What part of the correctness proof breaks down if the graph contains negative weights?)
The run time depends on the implementation of the priority queue.

If binary min-heaps are used:
With Fibonacci heaps (which were developed specifically to speed up this algorithm), O(V lg V + E) is possible. (Do not use this result unless you are specifically using Fibonacci heaps!)