Objectives
The objectives of today's experiment is to familiarize you with several basic methods of vector addition, including:

• The Graphical Method (also known as the parallelogram method)
• The Analytical Triangle Method
• The Analytical Component Method

Notes on Chapter 3
pp 13 - 23 of your lab book

A vector is a quantity which has both magnitude and direction. (Examples: displacement, velocity, acceleration, force)
A scalar is a quantity which has only a magnitude but no direction. (Examples: mass, temperature, energy, time)

A vector is represented graphically by an arrow.  Mathematically, there are many kinds of notation for vectors.  One way to distinguish a vector is by drawing an arrow on the top of a variable, .  Sometimes vectors are distinguished by using boldface, underline, or italics. I will underline all vectors, V, and I will use the "hat" or carat (^) notation to distinguish unit vectors, (this funny symbol is called "i-hat").  (Unit vectors are vectors whose magnitude is one unit).

A scalar adds normally. It is correct to say that 3 kg + 6 kg = 9 kg.
On the other hand, vectors do not add in the normal way.  It would be incorrect to say 3 mph, north + 6 mph, west = 9 mph, north-west.

How do vectors add?

1. The graphical method:

This method uses a graph to determine the result of A + B . It requires a ruler and protractor.  

Example: I want to add the vectors A = 3 mph, north and B = 6 mph, west.

Draw both vectors on a graph.
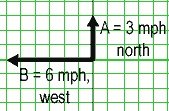
Copy the vector B and move the copy to the tip of the vector A , without changing the angle of B . Copy A and move it to the tip of vector B.  I now have a parallelogram.
Draw an arrow from the tail of (the original) A to the tip of B .  This is the resultant vector, R.

 If you measure the length of R, you will get about 6.7 mph (because the scale is in mph). This is the magnitude of R.  The magnitude of a vector is a scalar, and is written with no underline, R.  If you measure the angle, you will find it is about 153 degrees from the x axis.

2. The Analytical Triangle Method:

This method uses the law of sines and the law of cosines to solve for R, given two arbitrary vectors A and B . I will not emphasize this method. If you wish for me to show you how these equations come about, I can do this in class or you can ask me during my office hours. This method is not used very often, although I will ask you to remember the formulae below for the quiz next meeting.

Given a vector A and a vector B with a known angle  between them, (See Figure 3.2 on pg. 15)

the squared length of the resultant vector is R² = A² + B ² + 2AB cos .

the angle of the resultant vector is = sin^-1(B sin /R), where is measured from the vector A.

3. The Analytical Component Method:

This method finds the resultant vector by first splitting up the vectors into components. While vectors do not add normally, similar components do!

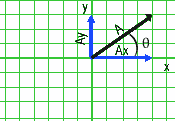
Split up the vector A into x and y components. If you are given the angle then you can easily calculate Ax and Ay, the x and y components of A. Ax = A cos Ay = A sin
Split up the vector B into components. Bx = B cos By = B sin
Now add together the components.  Components add normally. Rx = Ax + Bx Ry = Ay + By The squared magnitude of the resultant is R 2 = Rx2 + Ry2 The angle of the resultant vector is given by angle = tan-1(Ry/Rx) (Beware your calculator returns a value of -90 to 90 degrees for tan-1) This resultant vector is shown in black on the graph

The Force Table

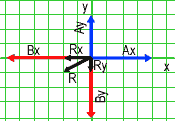
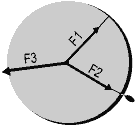
A force is a push or pull.  Forces are vectors.  Since they are vectors, we will add forces using the three methods above and compare these values with the measurements we make.  The force we will use is the force of gravity acting on mass (also known as weight).

We will add these forces by hanging a rope with a mass attached to it on a circular table we will call a force table.  We will have two masses which we want to add and a third mass which is used to balance the summed force.  If the apparatus is in balance, then the third force and the summed force are equal in magnitude.

Procedure:

There are pulleys which can be placed at arbitrary angles.  Strings with weights will be placed on the pulleys.  Your job is to balance the three weights.

1. Place one of the pulleys at 47 degrees.
2. Load the string on this pulley with 130 gm.  Note that the hook you attach to the string is already 50 gm unless otherwise noted on the hook 
3. Place the second pulley at 296 degrees. 
4. Load it with 115 gm.
5. Use the third pulley to balance the first two. You can load it with any weights you wish and put it at any angle you wish. 
6. The apparatus is balanced if the post is in the center of the ring and the strings line up with the center of the ring (see pictures below).

RIGHT	WRONG post is not in the center	WRONG the strings are not aligned

7. Determine the uncertainties in mass and angle. How much mass can you remove before the apparatus is significantly shifted?  How much can you change the angle before the apparatus is significantly shifted? These are the uncertainties in mass and angle respectively .
8. Repeat steps 1 through 8 for R1 = (83 gm) g, angle = 123 degrees, R2 = (156 gm) g, angle = 266 degrees .
9. Using the graphical method and the component method find the two resultants. This is step 2 and 3 on pg. 19 and 20. You may work together on this part.
10. Use the force table to determine the angles of R1, R2, and R3, where R1 = (170 gm) g, R2 = (82 gm) g, and R3 = (125 gm) g. R1, R2, and R3 are in balance, so R1 + R2 + R3 = 0
    

Assignments:

1. Complete page 23 on your own. (I will write some hints on the board).
2. Answer question 1 and 4 on page 25.