Magnetic Fields:Hopefully you have learned in your lecture that the source of the magnetic field is a moving charge. If I have a current in a wire, it will produce a magnetic field, since a current is made by moving charges.
- Direction of the magnetic field
Theory: The direction of the magnetic field is given by the right hand rule
Measurement: The direction of the magnetic field can be measured using a compass. The compass points in the direction of the magnetic field. It does this because a compass is a magnet, and magnets feel a torque (rotating force) when it is placed in a magnetic field.
- Strength of the magnetic field,
Theory: To get the strength of the magnetic field of a collection of moving charges (currents), you must use one of the two laws available to you: The Biot-Savart Law or Ampere's Law. In 152, these equations are already solved to give you the magnetic field strength of certain current configurations, which are listed in your book.
Measurement: To measure the magnetic field strength, you can use a gaussmeter. A gaussmeter is a device which uses the Hall effect to give you a value of the magnetic field. (Consult your text for a full explanation of the Hall effect)In this lab, we will map the direction of the magnetic field lines using a compass. We will map the fields of a bar magnet and a solenoid, which both have a theoretical field (ideally) of a pure magnetic dipole, for fields outside (see the pre-lab). In the second part of the lab we will need to measure the magnetic field strength inside our deflecting solenoid (see next section). To do this, we will use a gaussmeter.
Magnetic Forces:
Charges that move are the source of magnetic fields, but not only that, charges that move in magnetic fields also feel a magnetic force. The magnitude and direction of the force that is felt by the charge is given by the Lorentz Force Law:
FB = q v x B
(underlined variable means that this is a vector quantity)
The x in this equation means cross product or vector product. The magnitude of this force is:
|FB| = q|v||B| sin
(where |FB| means the magnitude of the vector FB, q is the charge which is moving in the magnetic field, v is the velocity of the charge, B is the magnitude of the magnetic field strength, andis the angle between v and B.)
The direction of this force is given by the right hand rule. (Some students are confused with this right hand rule and the right hand rule which is used to determine the direction of the magnetic field. Actually all cross products have a "right hand rule" and it is always the same rule, but the values which is in the product are the values which determine how you use the rule.)
We will directly verify the right hand rule in the lab using a bar magnet as the source of the magnetic field, and we will use the cathode ray tube as the moving charges, as shown below. What direction should the electrons be deflected in this case, according to the right hand rule?

Answer: the electrons will be deflected into the page. When looking down at the screen (when the electron is coming out towards you) you should see the electron deflect to the left when you move the magnet close to the CRT.
We would also like to make a quantitative measurement of the deflection of the electron for magnetic deflections in the same way that we did for electric deflections. Unlike electric deflections, a constant magnetic field causes the charge to undergo circular motion rather than a parabola. Not only that, but the circular motion is perpendicular to the magnetic field. How big the circle is depends on the velocity of the charge, the magnetic field strength, the mass of the charge, and the amount of charge, as we see below:
centripetal force = mangetic force
FC = FB
mv2/R = qvBsin
if v and B are perpendicular
R = mv/qB
Here we see that if we can measure the radius of the circular path, we can easily find the ratio q/m, the charge-to-mass ratio. However, if we deflect the electrons as we did in the example above (with the bar magnet), there are two problems which arise. First, the bar magnet does not produce a constant magnetic field; it produces a field which varies in magnitude and direction from point to point. Second, we can't see the electron inside the CRT. We can only see the point where the electron hits the screen. This means that even if the bar magnet could produce a constant field, we still couldn't measure the radius, because we wouldn't know how much of the circle that the electron had travelled.
There are ways to do this. If you go to the second floor of Watanabe, along the hall you will see a photograph of some strange curly lines. These are the paths of charged particles (produced in a high energy collision) going through a special apparatus called a bubble chamber. We do have student versions of these, called cloud chambers, but this device is brittle and slightly dangerous because it requires liquid nitrogen to cool it down to the critical temperature, so we don't allow freshmen physics students to use these in general.
So what can we do? First, we need something that produces a constant magnetic field: a solenoid. Inside a solenoid, the field is nearly constant (in the same way that the electric field was nearly constant inside the capacitor). If we place the CRT inside the solenoid, the field will be nearly constant in the CRT. However, the field is not pointing down like it was in our original picture. The field will point along the axis of the CRT, as shown below.
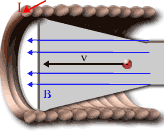
This presents another dilemma, however. The v and the B vectors are going in the same direction, so there is no magnetic force on the charge! So what do we do? Well, remember last time we used the cathode ray tubes? We learned that the electric deflection provided by the capacitor plates gave a velocity in the y direction! So here's what we'll do: we will first use electric deflection to get a velocity in the y direction. Then, having a velocity in the y direction, there will be a magnetic deflection in the solenoid.
We will analyze this situation in class in the same manner we did for electric deflection. At the end of the lecture, we will get the equation:
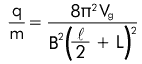
This is the charge to mass ratio of the electron. Note that the l and L in the equation are still the values found on pg. 39. The known value for the mass of an electron is 9.11 x 10-31 kg, and the charge of the electron is 1.6 x10-19 C. How does your experimental value compare?