Outline

• principles of recursion
• binary search
• more examples of recursion
• recursive linked list methods
• problem solving with recursion

Implementation of Recursion

• how can each invocation of the same method have a different copy of the parameter(s) and local variable(s)?
• several things must be remembered for each invocation:
  • the values of the parameters
  • the values of local and loop variables
  • the return address: the place where execution must resume once the method invocation is complete
• whenever a method is called, Java pushes all this information onto a system stack, which is not visible to the Java programmer
• whenever a method returns (or throws an exception), Java pops all this information from the stack, and starts executing code again from the return address (or the nearest matching catch)
• the stack works because execution of a method is entirely contained within the enclosing method, so the LIFO discipline is appropriate

Recursion instead of loops

• some programming languages don't even have loops, and use recursion instead
• any loop can be written as a recursive method:

  count = 0;
  for (int i = 0; i < 5; i++) {
    count = count + 1;
  }
  

  can be rewritten as:

  public int countToFive(int i) {
     if (i < 5) {
        return 1 + countToFive(i + 1);
     } else {
        return 0;
     }
  }
  ...
     count = countToFive(0);
  

Recursion structure

• infinite loops are not usually useful
• similarly, infinite recursion is not usually useful (and will result in stack overflow)
• so, every recursive method needs one or more base cases, for which it can compute the answer without using recursion
• every recursive method also needs one or more recursive cases

Breaking up a problem

• many problems have:
  • an obvious solution when they are small, and
  • a way to make a big problem into a smaller problem
• if this is the case, we can solve any size problem!
• for example, I know how to walk down one block
• assuming I can get to within one block of my destination, I know I can get to my destination
• so the smaller problem is, how do I get to within one block of my destination?
• recursion: first I must get to within one block of (one block from my destination)
• to get there, I must first get to within one block of (one block from (one block from my destination))
• etc.
• if I can always get one block closer to my destination, I am guaranteed to be able to get to my destination

recursive thinking: Binary Search

• can I break up a problem into one or more similar and smaller problems?
• example: find a number in a phone book
• one solution: search through all the numbers with while or for loops: this is an iterative solution
• a better solution: use recursion (recursive solution)
• if I am at the right entry, I know how to look it up
• the phone book is alphabetized
• if I have many entries, I can look at the middle one, and determine whether the entry I want is:
  • where I am looking: problem solved (a base case), or
  • before where I am looking: problem is smaller, or
  • after where I am looking: problem is smaller
• so, either I've solved the problem, or I can call the same method recursively to solve the smaller sub-problem
• for this problem, I actually have to keep track of the start and the end of the part of the phone book that might still have the desired name
• each time I look in the phone book, this part gets smaller
• at some point, this part gets so small that if I don't find the desired name, I know it is not in the phone book: this is the other base case for this recursive solution
• this is called binary search, because at each step I break the problem into two equal parts
• In-class exercise: what is the runtime of binary search?

Binary Search Implementation

/* @returns: the index of the item being searched, or -1 */
/* the element is between data[first] and data[last], inclusive */
public int binarySearch(int value, int [] data, int first, int last) {
  if (first > last) {          // base case: empty array
    return -1;
  }
  // if last >= first, last >= middle >= first
  int middle = (last + first) / 2;  // middle ~= first + (last - first) / 2
  if (data[middle] == value) {    // base case: found
    return middle;
  }
  if (data[middle] < value) {  // first recursive case: value in upper half
    return binarySearch(value, data, middle + 1, last);
  } else {  // second recursive case: value must be in the lower half
    return binarySearch(value, data, first, middle - 1);
  }
}

• reminder: binary search only works if the underlying array is in order
• how can I guarantee that this binary search code terminates?

Proving that a recursive method terminates

• prove that every recursive case gets closer to a base case
• for example, in binary search:
  • the base case is when the value is found, or first > last
  • on each recursive call, either first moves towards last, or last moves towards first, by at least one: because middle is not less than first, middle + 1 is bigger than first, and because middle is not greater than last, middle - 1 is less than last
• in general, must prove that the recursive case approaches the base case
• for factorial, a correct proof would depend on whether the base case is (n <= 1) or (n == 0) -- if the latter, the recursion does not terminate for n < 0

Details: comparing objects

• most objects have an absolute ordering
• for example, Strings or Integers
• we can rewrite the binary search code to compare an array of Object values
• to a target value defined to implement the Comparable interface:

  int compareTo(T value);
  

• x.compareTo(y) returns:
  • a value less than zero if x < y
  • a value of zero if x == y
  • a value greater than zero if x > y
• this can be used instead of the integer comparisons in the binary search method
• See the BinarySearch class

example: print an integer

• print the digits of an integer, separated by blanks
• must print the most significant digit first
• very easy to do recursively:

      private static void printInt(int toPrint) {
  	if (toPrint < 10) {            /* first (or only) digit */
  	    System.out.print(toPrint + "  ");
  	} else {
      /* print the digits before this one */
  	    printInt(toPrint / 10);
      /* print last digit -- could call printInt again recursively */
  	    System.out.print(toPrint % 10 + " ");
  	}
      }
  

• this code reaches the base case (toPrint < 10) before printing anything
• once the base case is reached, the remaining digits are printed after the inner call completes
• See also the complete program.

Reminder: how does recursion work?

• suppose I call printInt(8)
• no recursion is needed -- the first condition is true
• suppose I call printInt(82)
• the first condition is false, so the else clause executes
• printInt(8) is called, just as before
• what is the value of toPrint?
  • each invocation of printInt has its own value of toPrint
  • so the first invocation has toPrint = 82
  • the second invocation has toPrint = 8
  • although the two parameters called "toPrint" have the same name, they are parameters to different calls of printInt
  
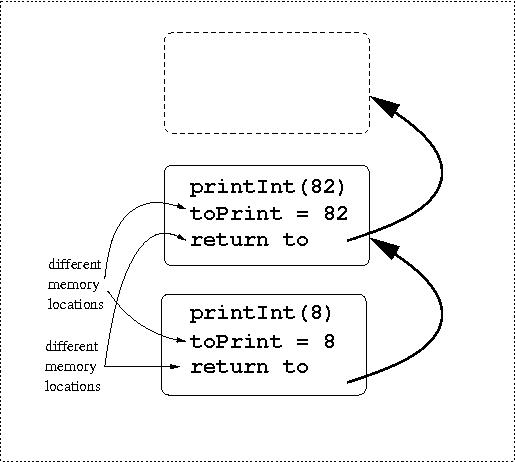
• similarly, we can trace this Recursive program

In-class exercise

• write a recursive method
• to print integers
• printing a comma every 3 digits
• for example, 1,234,567,890

computing fibonacci numbers

• the fibonacci sequence is 1, 1, 2, 3, 5, 8, 13, 21, ...
• the n-th fibonacci number fib(n) is simply defined as fib(n-1) + fib(n-2)
• this is clearly a recursive definition
• fib(1) == fib(2) == 1

     static int fib(int n) {
       if (n <= 2) {
         return 1;
       }
       return fib(n - 1) + fib(n - 2);
     }
  

• the only problem is this is very inefficient: computing fib(100) must compute fib(99) and fib(98).
• but computing fib(99) also recomputes fib(98), as well as fib(97)
• there are ways around this -- instead of computing from the large numbers, compute the small values first

efficient computation of fibonacci numbers

• the efficient way to compute fibonacci numbers is to start low and use the previous results in computing the new value
• this can be done either recursively or in a loop

  public static int fib(n) {
     if (n < 2) {
       return 1;
     }
     fibHelper(1, 1, n - 2);
  }
  private static int fibHelper(first, second, n) {
     if (n == 0) {  // base case, end of recursion
       return first + second;
     }
     return fibHelper(second, first + second, n - 1);
  }
  

• this recursive solution only takes linear time

  public static int fib(n) {
     int first = 1;
     int second = 1;
     while (n >= 2) {
       int third = first + second;
       first = second;
       second = third;
       n--;
     }
     return second;
  }
  

• the iterative solution also only takes linear time
• in-class exercise: convince yourself that the iterative and recursive solutions both compute the sequence 1, 1, 2, 3, 5, 8, 13, 21, ... (or find any bugs)

recursive data structures

• a linked list is essentially a recursive data structure: each node within a linked list is the head of a (perhaps smaller) linked list
• it is easy to write recursive linked list methods
• for example, to add, just return the new linked list with the new value inserted
• to remove, each recursive call can return the new linked list with the given value removed
• the implementation of LinkedListRec.java differs from the implementation in the book (and in my opinion, is simpler and clearer)
• returning a new linked list, even it if is identical to what was passed as a parameter, is a very powerful operation

problem solving with recursion

• many classical puzzles have recursive solutions
• for example, there is a game, Towers of Hanoi, which has three pegs and a number of discs of varying size
• each disk can go on any peg
• the game starts with all the disks on one peg
• disks are moved one at a time
• any disk D can be moved to any peg on which the topmost disk is larger than D
• the objective of the game is to move all the disks from one peg to another
• see here for an example of the actual game
• it has been said that there are monks in a monastery in Hanoi patiently engaged in moving 64 disks from one peg to another -- when they are done, the world might come to an end
• if this were true, how long would it take for the world to come to an end?

Solution to the Towers of Hanoi

• it is easy to move the smallest disk from one peg to another
• it is easy to move any disk D to another peg where the topmost disk is larger than D
• how do we move a set of n disks from peg 1 to peg 2?
• assume (recursively) that I know how to move a set of n-1 disks from peg 1 to peg 3
• and also from peg 3 to peg 2
• then, I do the first step (move the n-1 disks), then move the nth disk from peg 1 to peg 2, and finally move the n-1 disks back from peg 3 to peg 2
• of course, to move the n-1 disks from peg 1 to peg 3, I have to move the top n-2 disks from peg 1 to peg 2, then move the n-1th disk from peg 1 to peg 3, and finally move the n-2 disks from peg 2 to peg 3
• I can continue this until my base case, n == 1, where I can move the disk directly
• This is very easy to do recursively, and much harder to do iteratively
• See Towers.java

Finding a path through a maze

• finding a path through a maze is easy:
  • at the exit, conclude that the path has been found
  • at a dead end, conclude that the path has not been found
  • whenever there is a choice, recursively explore all choices
  • after marking the current location so we will not explore it again
• a tricky part of this is to find ways to mark a location so we can tell, when we visit it, whether it is:
  • known to be part of the path, or
  • known to have been visited already, or
  • not visited yet
• this requires a few bits at each position in the maze
• the program in the book represents these using colors

Backtracking

• finding a path through a maze is an example of a technique called backtracking
• if we have several choices, and we are not sure which one will work, we try one of them, and look at the result
• if the result is not favorable, we try the next choice
• this is done recursively, because we have more choices once we have made the first choice
• this can be useful in some games, such as chess or go
• however, exhaustively searching all possible moves is impractical
• instead, the search goes up to a point, estimates how good the play is at that point, and reports that
• in a two-player game, have to consider my best move in response to my opponent's best move -- my opponent's best move is the one that gives the lowest score, my best move is the one that gives the highest score

garbage collection

• garbage collection is easy:
  • start with the system stack and all the global variables
  • follow each of the pointers, marking each location as visited
  • at the end, any location that has not been visited, is free and can be reused
• we need to mark each of the memory areas as being in use or not
• one bit (or two colors) is sufficient