Outline

• trees
• binary search trees
• tree traversal
• binary node class
• binary search tree algorithms: add, remove, traverse

trees

• imagine having to store, in an organized fashion, all the descendants of a given person
• as in this family tree:
  image by Derrick Coetzee, in entry " family tree" in Wikipedia
• trees can hold any kind of data, even numbers:
  image by Derrick Coetzee, in entry " Tree (data structure)" in Wikipedia
• a node in a tree is similar to a node in a linked list, except:
  • a linked list node has a reference to zero or one other link nodes, whereas
  • a tree node has a reference to zero or more other tree nodes
• later we will consider how trees are implemented

Tree properties

• a tree has one root node, from which all other nodes can be reached by following links
• each node in a tree, except the root node, has exactly one parent
• each node in a tree can have zero or more children
• the other children of a node's parent are the node's siblings
• nodes are in a hierarchical relationship:
  • node X is an ancestor of another node Y, or
  • node X is a descendant of another node Y, or
  • node X is on a different branch than node Y
• nodes without children are leaf nodes
• nodes with children and a parent are interior nodes

Tree properties exercise

image by Derrick Coetzee, in entry " Tree (data structure)" in Wikipedia
• in-class exercise: identify the
  • root node
  • interior nodes
  • leaf nodes
  • parent of node 6
  • children of node 6
  • ancestors of node 5
  • descendants of node 7

more tree definitions

• a subtree is a node with all its descendants
• the level of a node is the number of its ancestors, so e.g. the root is always at level 1:
  • the children of the root are at level 2
  • their children are at level 3
  • the children of a node at level n are at level n+1
  sometimes the word depth is used instead of level
• the height of a tree is the maximum depth of any node in the tree
• in a binary tree each node has at most two children
  --- likewise, in a ternary tree each node has at most three children

types of binary trees

• in a balanced binary tree the depth of each subtree of every node differs by at most one (this is a recursive definition)
  --- there are also other definitions of balanced binary trees
• in an expression tree, each internal node contains an operator, and each leaf node is an operand (value)
  --- subtrees are evaluated first, yielding a value. Once all its children have been evaluated, we can evaluate a node
• in a Huffman tree, each internal node has two children. Each leaf node represents something to encode, such as a letter. The binary string to encode the letter is found by going down the tree from the root to the leaf. Each time we go left contributes a 0 bit to the code, and each time we go right contributes a 1 bit to the code.
• in a binary search tree each node has a value greater than every node in its left subtree, and less than every node in its right subtree
• in a full binary tree, each node has either 0 or two children
• a perfect binary tree of height n has 2ⁿ - 1 nodes, of which 2^{n - 1} are leaves
• a complete binary tree is a perfect binary tree up to the last level. All the leaves at the lowest level are as far to the left as possible.

binary search trees

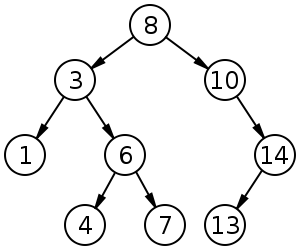
image by Derrick Coetzee and Booyabazooka, in entry " Binary search tree" in Wikipedia
• in-class exercise: how do we know this is a binary search tree?
• binary search (for value x) is now much easier:
  • if the value in the root is x, we are done
  • otherwise, if x < the value in the root, search (recursively) in the left subtree
  • otherwise, x > the value in the root, so search in the right subtree
  • if the subtree we need to search is empty, x is not in the tree
• in-class exercise: what is the runtime of this algorithm?

binary tree traversals

• if we want to visit each node in a binary tree, we have a choice of how to do it:
  • preorder traversal: visit the root node, then recursively visit the left subtree, then the right subtree
  • inorder traversal: recursively visit the left subtree, then visit the root node, then recursively visit the right subtree
  • postorder traversal: recursively visit the left subtree, then the right subtree, then the root node
• in-class exercises: do a pre-order, in-order, and post-order traversal of this tree, writing down node values in the appropriate sequence
  image by Derrick Coetzee, in entry " Tree (data structure)" in Wikipedia
• in-class exercises (individually): do a pre-order, in-order, and post-order traversal of this tree
  image by Derrick Coetzee and Booyabazooka, in entry " Binary search tree" in Wikipedia

Expression trees

• an expression tree is a tree where:
  • every node with children is an operator
  • every leaf node is an operand
• each operator operates on the values of its children
• in-class exercise: do a pre-order, in-order, and post-order traversal of this tree

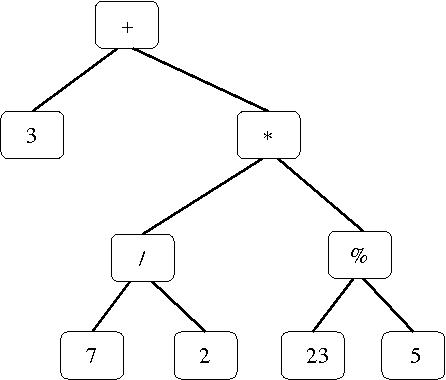
Binary search tree properties

• adding, finding (get), or removing a node are all O(depth), which, if the tree is balanced, is O(log n), with n the number of nodes
• compare to a sorted array, where binary search means finding is always O(log n), but inserting is O(n)
• binary search trees are an efficient way to search data and to sort data, as long as the trees remain balanced
• an unbalanced binary tree might look like a linked list
• in-class exercise: what is the runtime of the get method when the tree is not balanced?
• data can be identified with a unique key
• in-class exercise: add everyone's name to a search tree (in groups of five-ten people)
• in-class exercise: is the resulting tree balanced?

Binary node class

• a singly-linked list node has (at most) one reference to another node
• a binary tree node has (at most) two references to other nodes
• for example, see here
• both types of nodes also need a reference to the locally stored value
• data fields are item, left, right
• in-class exercise: build the following tree using the class BinaryNode
• in-class exercise: write a recursive static method to print the tree in postorder

Binary search tree add operation

• if key is less than the key of the current node, recursively add to the left subtree
• if key is greater than the key of the current node, recursively add to the right subtree
• otherwise, add at this node:
  • if there is no current node, create one and return it
  • if there is a current node, replace its contents with the new contents
• this assumes:
  • the method returns a new root for the new (sub)tree with the desired value inserted
  • the caller of this method knows what to do with the new root
• in-class exercise: create a new binary tree using as keys the following letters, in the order given: "hello world". These keys each carry the value 1, 2, 3, 4, 5, 6, 7 8, 9, 10, 11

Binary search tree remove operation

• find node with the given key
• if the node is a leaf node, just delete it, return null
• if the node only has a left subtree, return the left subtree
• if the node only has a right subtree, return the right subtree
• if the node has both subtrees, must replace it with another node that fits in the slot

Removing a node that has both subtrees

• the rightmost node in the left subtree can be put in place of the current node without altering the sorted property
• likewise, the leftmost node in the right subtree can be put in place of the current node
• that node might have a left (right) subtree, which can be used in its old position
• the rightmost node in the left subtree is the inorder predecessor of the current node
• the leftmost node in the right subtree is the inorder successor of the current node
• so either can be used
• in-class exercise: delete node 17 from this tree:
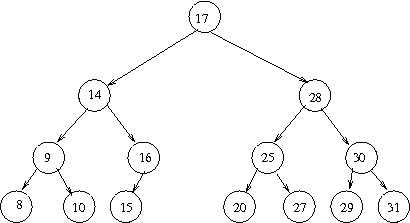
• in-class exercise (individually): delete node 14 from the original tree
• in-class exercise (individually): delete node 31 from the original tree