Outline

• queue implementation: linked queues
• queue exercises
• binary search
• trees
• binary search trees
• tree traversal
• binary search tree algorithms: add, remove, traverse
• binary node class

queue implementation strategies reminder

• similar to stack
• linked list implementation
• array implementation
• as always, we don't need to know the type of the elements, only that they are objects

naive linked list implementation of queues

• like stack: store all the elements in a linked list
• can keep two node references, to the first and to the last node in the list
• when the list is empty, these two references will be null
• when the list has one node, these two references will be to the same node
• at other times, these two references point to different nodes

linked list implementation of queues

• these many conditions (0, 1, or multiple nodes) make coding more difficult, and make it easier to make mistakes
• instead, have a single pointer, to the last node of the queue
• in a linked list, this node would have a next field with a value null
• for our queue, instead, this next field can point to the first node of the queue
• now, only two conditions: empty or non-empty queue
• in-class exercise: draw a linked queue with five nodes
• implementation is at LinkedQueue.java

runtime and space

• in-class exercise: what is the runtime for offer()?
• in-class exercise: what is the runtime for poll()?
• in-class exercise: what is the runtime for isEmpty()?
• in-class exercise: how much space does LinkedQueue use?

actual runtime

• run LinkedQueueSpeed.java.html to find out what the actual run-time is
• example runtimes
• in-class discussion: are you surprised?

implementation comparison

• array queue has limited size, or requires reallocating arrays (and copying the data correctly)
• linked queue has flexible size, proportional to the number of items in the queue
• both are O(1) for each operation, or amortized O(1) for offer on the resizable array queue
• the O() runtime may not give us all the information we would like -- actual testing can be followed by profiling, where we find out where in our program we are spending time

Binary Search (reminder)

• suppose we have an array of n values in ascending order, or any other sorted order
• to find element x, can search through the entire array (linear search)
• or, might look in the middle of the array, at index n / 2, and see if x < a[n/2] (condition L)
• if condition L is true, then the value is found, if anywhere, at one of the indices 0..(n/2 - 1)
• otherwise, see if x > a[n/2] (condition G)
• if condition G holds, then the value is found, if anywhere, at one of the indices (n/2 + 1)..(n - 1)
• if neither L nor G holds, x == a[n/2], and our search is complete
• if either L or G holds, we repeat the binary search, either recursively or iteratively

recursive binary search

// return -1 if not found, or the index of the element if found
public int searchArray(T value, T a[], int firstIndex, int lastIndex) {
  int numElements = lastIndex - firstIndex + 1;
  if (numElements < 1) {
    return -1;
  }

  // assert(numElements > 0)
  int middle = numElements / 2 + firstIndex;
  if (value.compareTo(a[middle]) == 0) {  // found!
    return middle;
  }
  if (numElements == 1) {  // firstIndex == middle == lastIndex
    return -1;           // not a match
  }
  // assert(numElements > 1), so firstIndex < middle < lastIndex
  // assert(value.compareTo(a[middle]) != 0)
  if (value.compareTo(a[middle]) < 0) {  // in the first half of the array
    return searchArray(value, a, firstIndex, middle - 1);
  } else {                                  // in the second half of the array
    return searchArray(value, a, middle + 1, lastIndex);
  }
  // assert: cannot reach this point, must have returned somewhere above
}

• in-class exercise: what is the runtime of this method?
• in-class exercise: rewrite this as an iterative (looping) binary search
• in-class exercise: what is the runtime of the iterative method?

maintaining a sorted array

• suppose the sorted array (e.g. "cassette", "cd", "dvd", "vinyl") needs a new element, e.g. "iPod"
• to insert this new element in the correct position,
  1. find the location where it would belong (by modifying searchArray, above)
  2. shift all elements after this location up by one
  3. store the element in this location
• in-class exercise: what is the runtime of this algorithm?
• suppose the sorted values were kept in a linked list
• in-class exercise: what is the runtime of this algorithm?

trees

• imagine having to store, in an organized fashion, all the descendants of a given person
• as in this family tree:
  image by Derrick Coetzee, in entry " family tree" in Wikipedia
• trees can hold any kind of data, even numbers:
  image by Derrick Coetzee, in entry " Tree (data structure)" in Wikipedia
• a node in a tree is similar to a node in a linked list, except:
  • a linked list node has a reference to zero or one other link nodes, whereas
  • a tree node has a reference to zero or more other tree nodes
• later we will consider how trees are implemented

Tree properties

• a tree has one root node, from which all other nodes can be reached by following links
• each node in a tree, except the root node, has exactly one parent
• each node in a tree can have zero or more children
• the other children of a node's parent are the node's siblings
• nodes are in a hierarchical relationship:
  • node X is an ancestor of another node Y, or
  • node X is a descendant of another node Y, or
  • node X is on a different branch than node Y
• nodes without children are leaf nodes
• nodes with children and a parent are interior nodes

Tree properties exercise

image by Derrick Coetzee, in entry " Tree (data structure)" in Wikipedia
• in-class exercise: identify the
  • root node
  • interior nodes
  • leaf nodes
  • parent of node 6
  • children of node 6
  • ancestors of node 5
  • descendants of node 7

more tree definitions

• a subtree is a node with all its descendants
• the depth of a node is the number of its ancestors, so e.g. the root always has depth 0:
  • some people prefer to say the root has depth 1, but in this class the root always has depth 0
  • the children of the root are at depth 1
  • their children are at depth 2
  • the children of a node at depth n are at depth n+1
• the height of a tree is the maximum depth of any node in the tree
• in a binary tree each node has at most two children
  --- likewise, in a ternary tree each node has at most three children
• in a balanced binary tree the depth of each subtree of every node differs by at most one
  --- there are also other definitions of balanced binary trees
• in a binary search tree each node has a value greater than every node in its left subtree, and less than every node in its right subtree

binary search trees

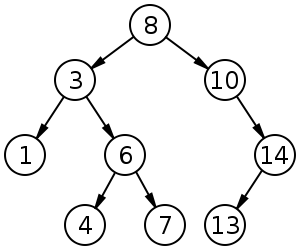
image by Derrick Coetzee and Booyabazooka, in entry " Binary search tree" in Wikipedia
• in-class exercise: how do we know this is a binary search tree?
• binary search (for value x) is now much easier:
  • if the value in the root is x, we are done
  • otherwise, if x < the value in the root, search (recursively) in the left subtree
  • otherwise, x > the value in the root, so search in the right subtree
  • if the subtree we need to search is empty, x is not in the tree
• in-class exercise: what is the runtime of this algorithm?

binary tree traversals

• if we want to visit each node in a binary tree, we have a choice of how to do it:
  • preorder traversal: visit the root node, then recursively visit the left subtree, then the right subtree
  • inorder traversal: recursively visit the left subtree, then visit the root node, then recursively visit the right subtree
  • postorder traversal: recursively visit the left subtree, then the right subtree, then the root node
• in-class exercises: do a pre-order, in-order, and post-order traversal of this tree, writing down node values in the appropriate sequence
  image by Derrick Coetzee, in entry " Tree (data structure)" in Wikipedia
• in-class exercises (individually): do a pre-order, in-order, and post-order traversal of this tree
  image by Derrick Coetzee and Booyabazooka, in entry " Binary search tree" in Wikipedia

Expression trees

• an expression tree is a tree where:
  • every node with children is an operator
  • every leaf node is an operand
• each operator operates on the values of its children
• in-class exercise: do a pre-order, in-order, and post-order traversal of this tree

Binary search tree properties

• adding, finding (get), or removing a node are all O(depth), which, if the tree is balanced, is O(log n), with n the number of nodes
• compare to a sorted array, where binary search means finding is always O(log n), but inserting is O(n)
• binary search trees are an efficient way to search data and to sort data, as long as the trees remain balanced
• an unbalanced binary tree might look like a linked list
• in-class exercise: what is the runtime of the get method when the tree is not balanced?
• data can be identified with a unique key
• in-class exercise: add everyone's name to a search tree (in groups of five-ten people)
• in-class exercise: is the resulting tree balanced?

Binary search tree add operation

• if key is less than the key of the current node, recursively add to the left subtree
• if key is greater than the key of the current node, recursively add to the right subtree
• otherwise, add at this node:
  • if there is no current node, create one and return it
  • if there is a current node, replace its contents with the new contents
• this assumes:
  • the method returns a new root for the new (sub)tree with the desired value inserted
  • the caller of this method knows what to do with the new root
• in-class exercise: create a new binary tree using as keys the following letters, in the order given: "hello world". These keys each carry the value 1, 2, 3, 4, 5, 6, 7 8, 9, 10, 11

Binary search tree remove operation

• find node with the given key
• if the node is a leaf node, just delete it, return null
• if the node only has a left subtree, return the left subtree
• if the node only has a right subtree, return the right subtree
• if the node has both subtrees, must replace it with another node that fits in the slot

Removing a node that has both subtrees

• the rightmost node in the left subtree can be put in place of the current node without altering the sorted property
• likewise, the leftmost node in the right subtree can be put in place of the current node
• that node might have a left (right) subtree, which can be used in its old position
• the rightmost node in the left subtree is the inorder predecessor of the current node
• the leftmost node in the right subtree is the inorder successor of the current node
• so either can be used
• in-class exercise: delete node 17 from this tree:
• in-class exercise (individually): delete node 14 from the original tree
• in-class exercise (individually): delete node 31 from the original tree

Binary node class

• a singly-linked list node has (at most) one reference to another node
• a binary tree node has (at most) two references to other nodes
• for example, see here
• both types of nodes also need a reference to the locally stored value
• data fields are item, left, right
• methods include constructors, accessor methods, mutator methods, toString
• test program builds small tree, tests the methods
• in-class exercise: build the following tree using the methods from class BinaryNode
• in-class exercise: write a recursive static method to print the tree in postorder