4F  Simple Interest Amortized Loans

We studied in Section B the so-called add-on interest loan, in which the interest charged each payment period is based on the original amount borrowed. These loans are more commonly entered into for moderately priced consumer items. For much larger purchases – such as in buying homes or new cars, for example – the simple interest amortized loan is the standard. With this type of loan, interest is paid only on the outstanding balance. As the borrower makes payments on the loan, the outstanding principal on the loan decreases, and accordingly the amount of interest being paid likewise decreases. But the amount of each payment remains the same, so as time goes on more of each payment is used to pay down the principal and less is used to pay off the interest.

We use the following notation in our calculations with simple interest amortized loans:

The formula for the amount of each payment on the loan is

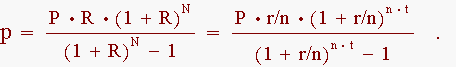
In the vast majority of home mortgages, payments are made on a monthly basis. For such loans the number of payments per year is n = 12, while the periodic interest rate is the annual interest rate divided by 12, or R = r/12. The formula for the monthly payment then becomes

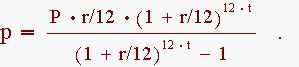
example 1

Lucky and Lucille borrowed $20,000 to buy a car, getting a simple interest amortized loan with a 12% annual interest rate, and with payments to extend over 3 years. We calculate their monthly payment, the sum of all their payments, and the total interest they will pay.

The principal is P = $20,000, the periodic interest rate is R = 12%/12 = 1% = .01, and the number of payments is N = 12 · t = 12 · 3 = 36. The monthly payment formula gives

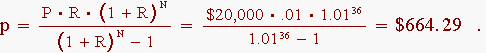
As they will make 36 payments of this amount, the total sum of money they will pay to the lender over the life of the loan is

The total interest they will pay is the difference in what they pay back and the principal they borrowed,

Now we prepare a so-called amortization schedule for the first three payments of the loan in the previous example. The periodic, or monthly, interest rate on the loan is R = 12%/12 = 1% = .01; thus Lucky and Lucille must each month pay 1% interest on the outstanding balance on the loan. Using the simple interest formula, we calculate the interest for the first month as

This amount comes out of their first payment, and the remainder,

is applied to pay off the principal. Thus, after the first month the outstanding principal, or balance, is

For the second month, the interest on the outstanding principal is

This amount comes out of the second payment, and the remainder,

is applied to the principal; the new balance on the principal is the difference

Finally, for the third month the interest is

the amount applied to the principal is

and the outstanding balance after the third month is

We summarize the above calculations in an amortization table:

A complete amortization table would continue through all 36 payments, until after the last payment the balance reduces to zero.

example 2

The Nakashima family will borrow $240,000 to buy a house in Kailua on Enchanted Lake. From American Savings they can get a loan at a 7% annual interest rate, with monthly payments stretched over 30 years. We will calculate the

1. monthly payment,
2. total amount of all payments,
3. total interest to be paid on the loan.

Finally, we will construct an amortization table for the first three months of the loan.

We substitute P = $240,000, r = 7% = .07, and t = 30 into the payment formula and find that the amount of the monthly payment is

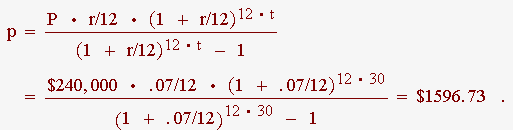
In 30 years there will be 12 · 30 = 360 payments, and the total of all payments will be

Finally, the interest the family will pay over the life of the loan is the difference

Now, to make the table, we compute the first month's interest as

The amount of the first payment applied to principal is

and the balance on the principal after one month is

For the second month the interest is

the amount applied to principal is

and the new balance is

We repeat this procedure for the third month. You can check that the calculations for the third month are as displayed in the table:

EXERCISES 4F

1. Having found the home of their dreams, the Howe family is looking into financing. They must borrow $200,000 to purchase their new house. Calculate their monthly payment under the following plans:
   1. 15 year loan, 6% annual interest rate,
   2. 20 year loan, 6.3% annual interest rate,
   3. 25 year loan, 6.6% annual interest rate,
   4. 30 year loan, 7.2% annual interest rate.
   Also, under each plan calculate the sum of all their payments, as well as the total interest they will pay.

Mr. Brewster is pleased to have just purchased a brand new car, financing it with a $30,000 loan at a 12% annual interest rate, with payments to be made over 5 years. Calculate his monthly payment, the total of all his payments, the total interest he will pay. Also, construct an amortization table for the first three payments.

3. A church on Molokai will borrow $100,000 for remodeling. Through First Hawaiian Bank the church can get a 20-year loan at a 6% annual interest rate. Construct an amortization table for the first four monthly payments.